This document discusses how grades are curved in Canvas when the Curve Grades option is selected in the Gradebook. This process is detailed in three parts: constructing the bell curve, calculating final scores, and distributing student scores within the curve.
Canvas allows instructors to curve grades for individual assignments. To curve grades, select the Curve Grades option in the Gradebook. Canvas asks for an average score and then adjusts the scores along a bell curve around that score. Student grades will be impacted differently based on where they are in the distribution of scores. Perfect scores will not be affected by curving grades.
In the academic community, curving grades is advisable if only a certain number of students can pass, or when you require a fixed distribution of grades distributed throughout the class. Grade curving cannot be undone. Pre-curved grade histories will be available, but the curving action is irreversible.
This document explains how grades are curved when this option is used. This process is detailed in three parts: constructing the bell curve, calculating final scores, and distributing student scores within the curve.
Constructing the Bell Curve
The first step to constructing the bell curve is identifying the maximum score, average score, and minimum score. The maximum score is simply the total amount possible for that assignment. The average score is the score the instructor inputs in the Curve Grades dialogue box (see image below).
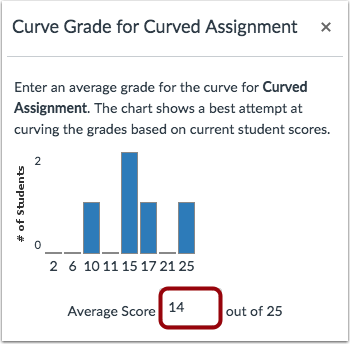Curve Grades in Canvas
To calculate the minimum score, follow the four steps below:
- Divide the average score by the total points possible
- Multiply the result by two
- Subtract one
- Multiply the result by the maximum score
For example, consider an assignment with 25 total points possible and an average score of 14.
- 14/25 = 0.56
- 0.56 x 2 = 1.12
- 1.12 - 1 = 0.12
- 0.12 x 25 = 3
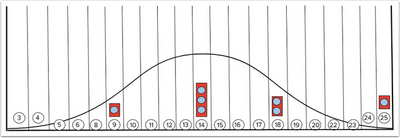
The bell curve Canvas uses to curve grades is divided into twenty-one sections, called curve targets [1], using twenty-two break points [2]. The minimum score is represented by the far-left break point [3] and the maximum score by the far-right break point [4]. The average score will fall within the middle curve target [5].
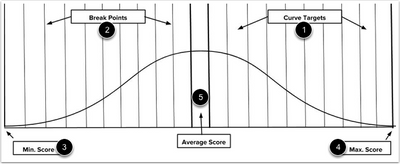View Bell Curve
Each break point represents a percentage of student scores that can be placed inside the curve moving from right to left, allowing for an equal distribution of scores within the curve.
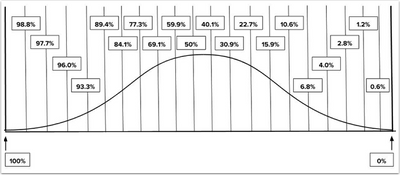View Break Points
For example, the break point that represents 6.8% designates that up to 6.8% of student scores can be placed within curve targets to the right of that break point.
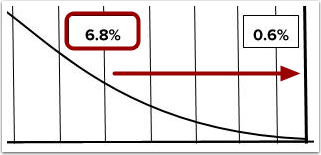Example Break Point
Calculating Final Scores
Each curve target is assigned a final score by equally distributing scores between the minimum and maximum scores. To calculate the difference between each curve target, follow the steps below:
- Subtract the minimum score from the maximum score.
- Divide that total by the remaining break points.
- Using this number as the difference between break points, assign a decimal score to each break point.
- Round each decimal score to the nearest whole number.
In our example from the previous section, we identified the minimum score as 3 and the maximum score as 25. Below are the steps for these numbers:
- 25 - 3 = 22 from 25
- 22/19 = 1.16.
- 3 + 1.16 = 4.16; 4.16 + 1.16 = 5.32; 5.32 + 1.16 = 6.48; 6.48 + 1.16 = 7.64; etc.
- 4.16 rounds to 4; 5.32 rounds to 5; 6.48 rounds to 6; 7.64 rounds to 7; etc.
The image below shows the final score given to each curve target.
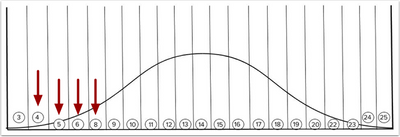Final Scores
Distributing Scores
The first step to distributing student scores within our bell curve is to group them within score bins. A score bin will include every student score that begins with the same integer. For example, scores of 15.1, 15.5, and 15.9 will be placed within the same score bin [1]. A score of 14.9 would be placed in a lower score bin [2] and a score of 16.0 would be placed in a higher score bin [3].
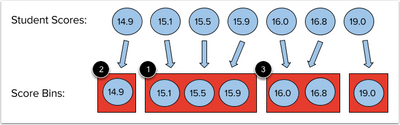Distributing Scores
Scores within the same bin will all be placed in the same location in our bell curve, which will result in the same final score for all submissions in that bin.
After all scores are placed in their respective bins, we must calculate the percentage of scores contained in a bin plus the percentage contained in all bins with higher scores. If the image on the previous page represented all scores, the bin that includes the 19.0 score would contain 14.29% (1/7) of all scores [1]. Moving to the bin that includes the 16.0 and 16.8 scores, we have now accounted for 42.86% (3/7) of all scores by adding the two scores in that bin to the one score in the first bin [2]. View the image below for a complete accounting of these scores.
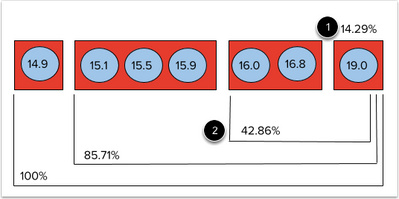View Distribution Scores
Our next step is to place score bins within the curve targets we defined in the first section. The top score bin is always placed within the first curve target. If the percent of scores in our first score bin accounts for less than 0.6% of all scores, the next score bin will also be placed within this curve target and receive a score of 100%. (This will continue until that 0.6% threshold is reached.) If the percent of scores in that bin exceeds 0.6%, the next score bin will need to be placed within a later curve target.
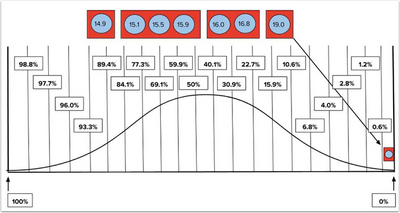View Distribution Bins
To determine where all the remaining score bins will be placed, we must look to the cumulative percentage we assigned to the previous bin. In the example in the images above, our second bin would be placed within the curve target that includes 14.29% [1]. (The sixth curve target, between 10.6% and 15.9%.) Our third score bin would be placed in the curve target that includes 42.86% [2] and the fourth score bin would be placed in the curve target that includes 85.71% [3].
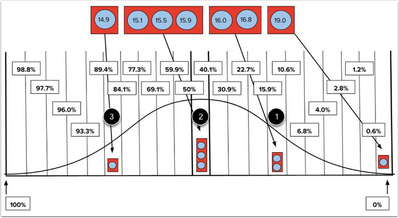View Curve Bins
Assuming a typical distribution of scores and enough students, the students in the score bin containing the pre-curved median score should get assigned to the middle curve target and be assigned the specified average score.
Combining the image on the previous page with the final scores calculated in the Calculate Final Scores section, we can see the final scores assigned to student submission after grades are curved.
Distribution Score Bin
Last update: 2017-01-07
This resource can also be accessed from the following Canvas Guides:
